The previous articles in this Greek textbook series looked at Delta and Gamma, which are the first and second order sensitivities of an option or structured product price with respect to the underlying asset. These are the most important and direct of the Greeks as hedging the underlying asset as its price changes is fundamental to the concept of how derivatives and their pricing work. The simplest option pricing models such as Black-Scholes assume constant values for other important parameters such as volatility, interest rate and dividend yield but they allow for changes in the underlying.

However in practice all pricing parameters that go into option pricing continuously change, just like any other economic variable. The first of these that we will consider is sensitivity to the volatility level, known as “Vega”.

The role of Vega in risk management

Because volatility is so important to option pricing we can understand that hedging any changes will be crucial to effective risk management. Any product which has a long option position such as a protected growth product will have positive sensitivity to volatility whereas those where the investor has capital at risk (for example a reverse convertible) will generally have negative sensitivity.

The value of Vega reflects the direction that the product price will take if volatility changes. From a trader’s perspective, these sensitivities translate into practical consequences because as volatility increases, the trader will generally have to do more rebalancing of the underlying as it moves around more.

If those rebalances happen in a way that the trader will incur cost (because of being forced to buy the underlying when it goes up and selling when it goes down) then the trader is exposed to volatility increasing and the value of the Vega will indicate that. This is known as being short Gamma and short Vega. The reverse would be true for a long Vega position.

In the previous articles we analysed Delta and Gamma for call and put options. The chart below shows the Vega exposure for a call and put option at the same strike price.

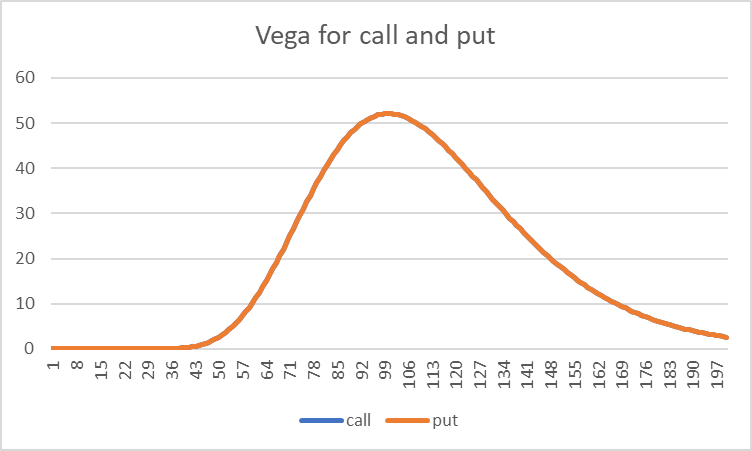
We immediately notice two things. Firstly the two curves are identical, meaning that vega is the same at all spot values for the call and put. Secondly we see that the shape of the curve is much like the Gamma chart and rises to a peak near the strike price.

Both of these properties of Vega can be explained.

The equal values of Vega for a call and put option of the same strike and maturity follow from the simple relationship known as put-call parity.

A call option pays

where S is the final spot price and K is the strike price

and a put option pays

By examining the maximum and minimum function we can see that for any final spot price S the payoff from a call minus the payoff from a put is equal to the difference between the spot and strike prices as follows:

Since this relation holds for any spot price S it follows that the equivalent relation also holds for the price of call and put

Where F is the forward price of the stock and A is the risk-free discount factor to the option maturity

Vega is the sensitivity of Call or Put to volatility, therefore we can further use this equality to take volatility sensitivity (differential) of both sides of the equation to get

The right hand side is zero since none of the terms F, K and A have any sensitivity to volatility

Finally we can deduce that Vega_Call = Vega_Put. This is an elegant and important result, and applies independent of any modelling assumptions.

Relationship between Vega and Gamma

The fact that the Gamma and Vega curves generally have the same shape is well known. Under the Black-Scholes model for calls and puts, the expression for Gamma and Vega are both analytic results and have a simple relation:

Where T is the remaining time in years. Since Gamma for a call or put rises to a peak, this will also be true for Vega, though the S^2 term means that the curve is not quite the same. The T term is also important, Vega reduces naturally with time left since changes in volatility have less time to affect the underlying distribution and therefore product outcome. For a product with multiple options, or under different modelling assumptions than Black Scholes this relation will not be exact but will still broadly be true.

Vega is an important Greek for Volatility management and is central to the idea of dynamic hedging of options as well as having strong connections with the related quantity of Gamma.